Brief Introduction to Quantum Mechanics

Schrödinger Equation

In quantum mechanics, a system is characterized by its wavefunction Ψ. The properties of the system are obtained by acting on the wavefunction with a property-specific operator. For example, the energy of a molecule can be obtained by solving the equation in which the Hamiltonian operator acts on the wavefunction. Such an equation is known as the Schröedinger equation:

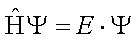
For many systems, including multi-electron atoms and molecules, the Schrödinger equation is difficult to solve because we do not know beforehand what the wavefunction of a complex system such as a molecule looks like. On the other hand, we do know how to write down the Hamiltonian operator for nearly any conceivable system. The Hamiltonian is a sum of the kinetic energy operator and the potential energy operator.

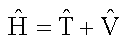
The potential energy operator corresponds to the classical interaction energies between particles in the system. In quantum mechanics, the kinetic energy operator involves a Laplacian, or the sum of unmixed second derivatives of the function with respect to the displacements. In the case of a one-variable function, the Laplacian is simply the second derivative of the function with respect to the displacement; the Laplacian and Hessian are identical when the motion is confined to one dimension. Thus, the Schröedinger equation is a second order differential equation. For example, the Schröedinger equation for a system that undergoes one-dimensional harmonic oscillations in quadratic potential around the equilibrium value can be written as:

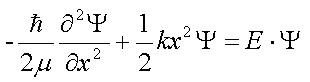
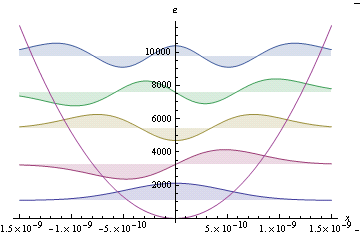
There are many possible solutions to the Schrodinger equation of a bound system. Each solution corresponds to a different energy state of the system. The discrete spectrum of solutions implies that only states with certain energy values are allowed. If the Hamiltonian is simple enough, the Schrodinger equation can be solved analytically. For example, the Schrodinger equation for the harmonic oscillator is analytically solvable; some of the wave functions and allowed energy levels are shown on the right. The harmonic oscillator is a good model for the analysis of vibrations of diatomic molecules. For example, we can see that the ground vibrational state has a certain non-zero energy, called the zero point vibrational energy. The ground state wave function is a gaussian function, and the most likely internuclear distance corresponds to no displacement from the equilibrium position. We also see that the spacing of energy levels is constant, and given by h ν for harmonic oscillator. Another exactly solvable problem is the hydrogen atom. Determination of the best value of ξ in the hydrogen atom via the variational principle in atomic units is illustrated in Mathematica notebook H_Atom_Vari_Slater_AU (also available as PDF). The accuracy of this solution can be appreciated by comparing the calculated and observed line spectra of the hydrogen atom. This requires solution in SI units and outlined in the Mathematica notebook H_Atom_Vari_Slater_AU (also available as PDF). For more complicated systems, only approximate solutions are possible.

To continue reading click on the link below:

https://people.chem.ucsb.edu/kahn/kalju/chem126/public/qm_intro.html